Sets

This post is an introduction to sets as mathematical objects. It is based on the book Introduction to Topology of Menselson [1]. It aims to give a visual introduction to sets theory.

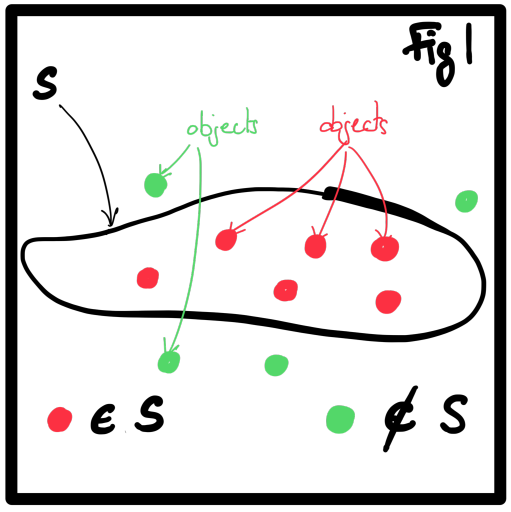
Roughly speaking, a set $S$ is an ensemble of objects. Let $x$ be an object. If $x$ belongs to $S$, we will note $x\in S$ and if $x$ does not belong to $S$, we will note $x\notin S$. We will also note $\{x_1,\dots ,x_n\}$ the set that contains the objects $x_1,\dots ,x_n$. The set that has no member is called to null (or empty) set and noted $\mathrm{\varnothing }$.

Figure 1: Sets

When all objects of a set $A$ also belongs to a set $B$, we say that $A$ is a subset of $B$ and we note $A\subset B$. Note that a set is always contained in itself and the same is true for the empty set $\mathrm{\varnothing }$, these are improper subsets. Others subsets are called proper subsets.

Figure 2: Sets inclusion

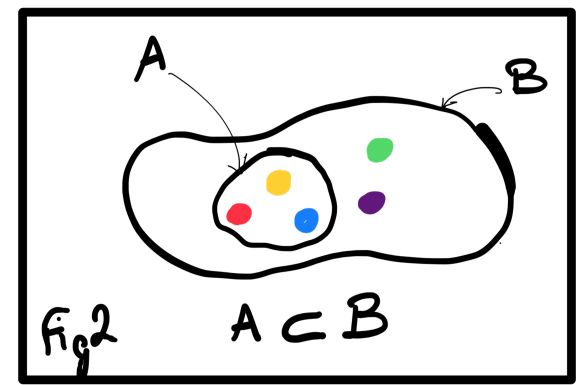
To compare multiple sets, we compare their elements. To show the equality of sets, it is usually a good idea to prove that each set is contained in each other.

Sets are also objects.

Power sets

The power set of $S$, noted $\mathcal{P}(S)$ or $2^S$, is a set that is the collection of all subsets of $S$. For each set $S$, the set $A\in \mathcal{P}(S)$ if and only if $A\subset S$.

Figure 3: Power sets

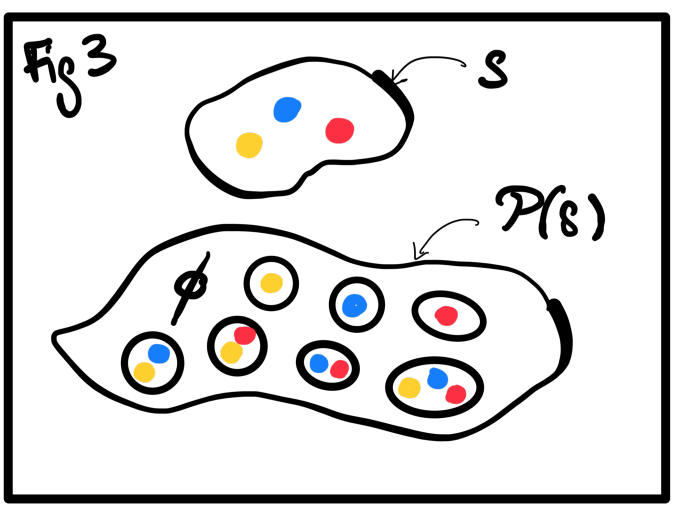
Some comments about sets:

• For each set $S$, $S\in \mathcal{P}(S)$ by definition but $S\not\subset \mathcal{P}(S)$ as the elements of $S$ do not belong to $\mathcal{P}(S)$. However, the set $\{S\}\subset \mathcal{P}(S)$ because all the elements of $\{S\}$, $S$ and $\mathrm{\varnothing }$, are in $\mathcal{P}(S)$.

• For each set $S$, $\mathrm{\varnothing }\in \mathcal{P}(S)$ by definition and $\mathrm{\varnothing }\subset \mathcal{P}(S)$ as the elements of $\mathrm{\varnothing }$ (there are none) are included in $\mathcal{P}(S)$.

• Consider $A,B$ and $C$. If $A\subset B$ and $B\subset C$, then $B\subset C$.

Figure 4: Multiple sets inclusion

Intersection, Union and Complement

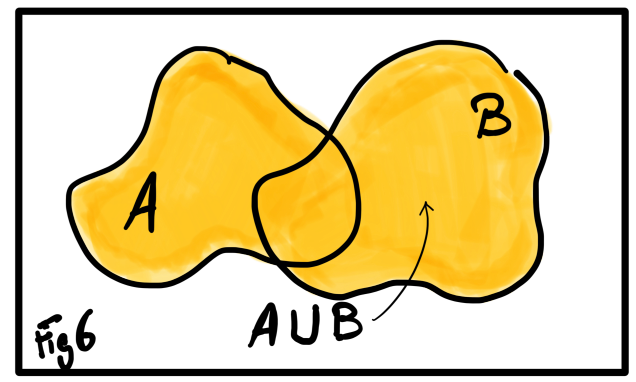
Let $A$ and $B$ be two sets. The set that contains elements that belongs to $A$ and to $B$ is the intersection of $A$ and $B$ and is denoted by $A\cap B$. The set that contains elements that belongs to $A$ or $B$ is the union of $A$ and $B$ and is denoted by $A\cup B$.

Intersection

Union

Figure 5: Intersection and Union

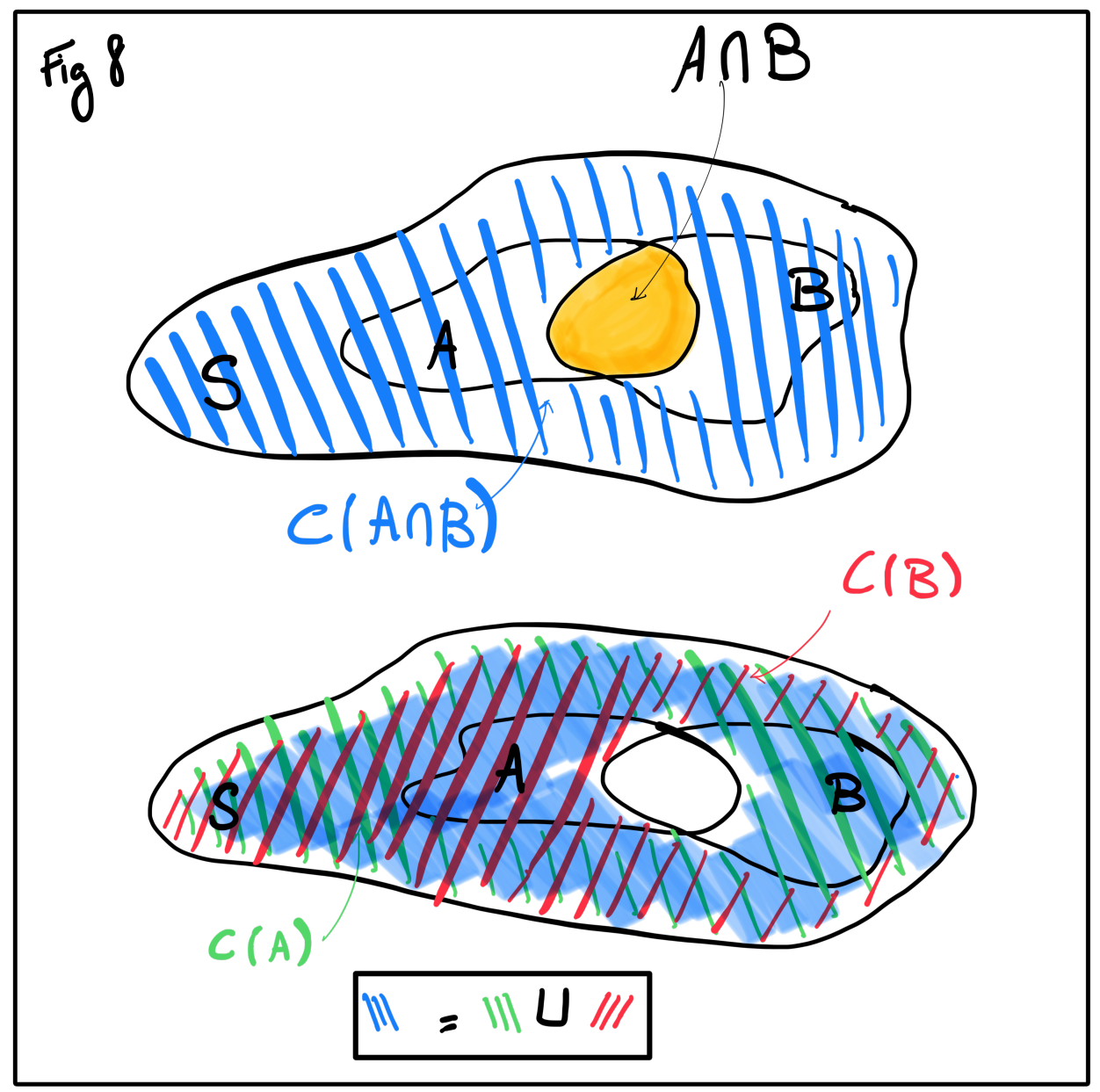
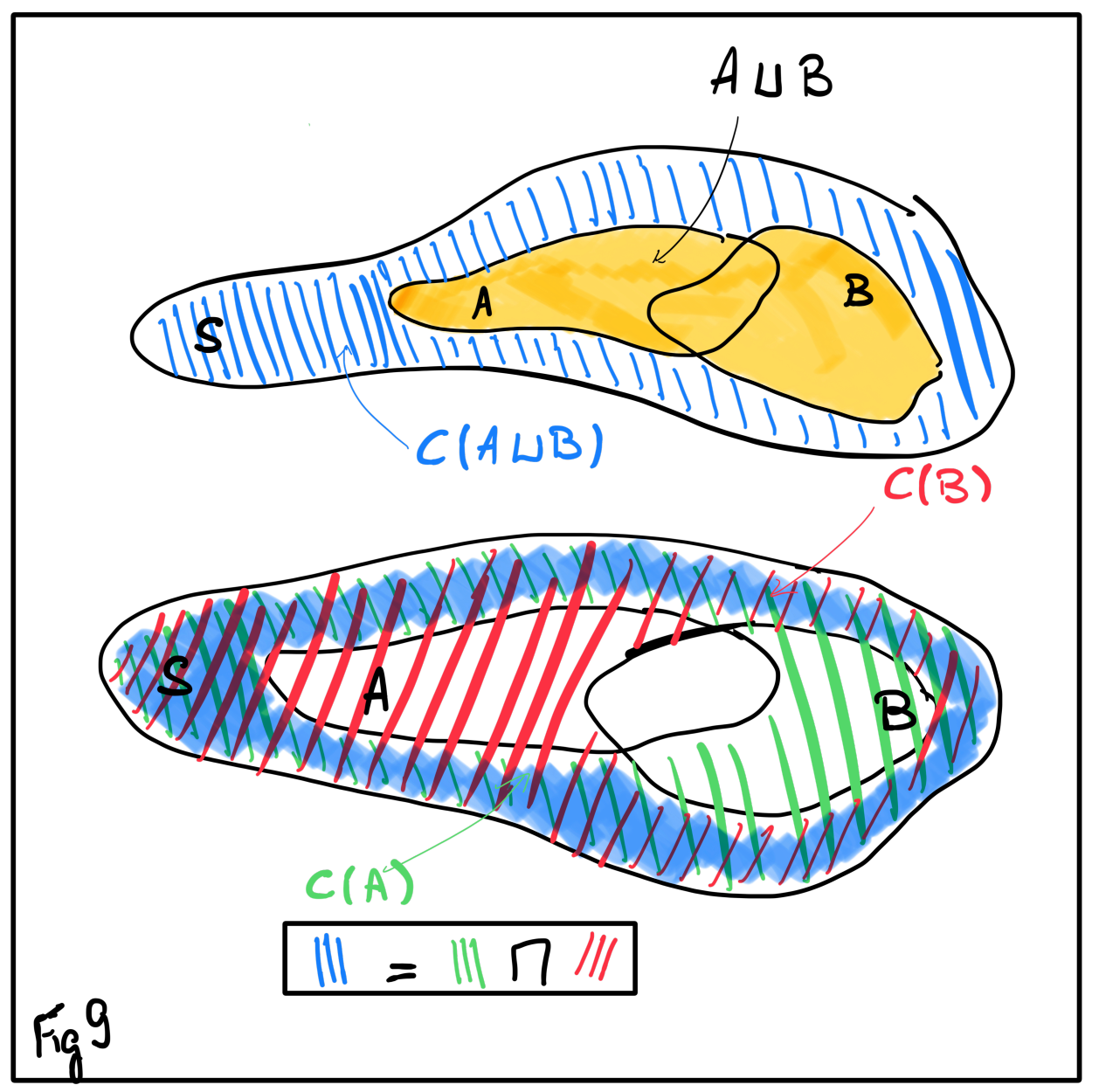
The complement of a set $A\subset S$ is the set of elements that belong to $S$ but not to $A$. It is denoted by $C(A)$. As $C(A)$ is a set, we can take its complement and recover $A$.

Figure 6: Complement

DeMorgan’s laws

DeMorgan’s laws are relations between the complement of the intersection of $A$ and $B$ (or the union) and the union of the complement of $A$ and the complement of $B$ (or the intersection of the complements). Mathematically, this is written, for $A$ and $B$ two sets:

• $C(A\cap B)=C(A)\cup C(B)$

Figure 7: Visual proof for the complement of the intersection

• $C(A\cup B)=C(A)\cap C(B)$

Figure 8: Visual proof for the complement of the union

References:

[1] Mendelson, B., 2012. Introduction to Topology: Third Edition. Courier Corporation.